[JAVA의 정석] Ch 2. 변수(Variable)
1. 변수와 상수
1) 변수
값을 저장할 수 있는 메모리상의 공간
하나의 변수에 단 하나의 값만 저장할 수 있으며, 새로운 값을 저장하면 기존의 값은 사라진다
2) 변수의 선언과 초기화
- 변수 타입 : 변수에 저장될 값이 어떤 타입인지를 지정하는 것
- 변수 이름 : 메모리 공간에 이름을 붙여주는 것
변수를 선언하면, 메모리의 빈 공간에 변수 타입에 알맞는 크기의 저장공간이 확보되고, 앞으로 이 저장공간은 변수 이름을 통해 사용할 수 있게 된다.
int age; // age라는 이름의 변수를 선언
- 변수 초기화 : 변수를 사용하기 전에 처음으로 값을 저장하는 것
변수를 선언한 이후부터는 변수를 사용할 수 있으나, 그 전에 반드시 변수를 초기화해야한다. 메모리는 여러 프로그램이 공유하는 자원이므로 전에 다른 프로그램에 의해 저장된 알 수 없는 값(쓰레기값)이 남아있을 수 있기 때문이다.
변수에 값을 저장할 때는 대입 연산자 '='를 이용한다. 오른쪽 값을 왼쪽(변수)에 저장하라는 뜻이다.
변수에 값을 저장하는 대입연산은 우변의 모든 계산이 끝난 후에 제일 마지막에 수행된다.
int age = 25; // 변수 age를 선언하고 25로 초기화한다
int year = age + 2000; // 변수 age에 저장된 값(25)일 읽어와서 식에 사용한다
3) 변수의 명명 규칙
'변수의 이름'처럼 프로그래밍에서 사용하는 모든 이름을 '식별자'라고 하며, 식별자는 같은 영역 내에서 서로 구분될 수 있어야 한다.
1. 대소문자가 구분되며 길이에 제한이 없다
- True와 true는 서로 다른 것으로 간주된다
2. 예약어를 사용해서는 안 된다
- true는 예약어라서 사용할 수 없지만, True는 가능하다
3. 숫자로 시작해서는 안 된다.
- top10은 허용하지만, 7up은 허용되지 않는다.
4. 특수문자는 '_'와 '$'만을 허용한다.
- $harp는 허용되지만, S#arop은 허용되지 않는다
- 예약어 : 프로그래밍언어의 구문에 사용되는 단어

- 자바 프로그래머들에게 권장하는 규칙
1. 클래스 이름의 첫 글자는 항상 대문자로 한다.
- 변수와 메서드의 이름의 첫 글자는 항상 소문자로 한다
2. 여러 단어로 이루어진 이름은 단어의 첫 글자를 대문자로 한다
- lastIndexOf, StringBuffer
3. 상수의 이름은 모두 대문자로 한다. 여러 단어로 이루어진 경우 '_'로 구분한다
- PI, MAX_NUM
2. 변수의 타입
1) 기본형과 참조형
- 자료형 : 값의 종류에 따라 값이 저장될 공간의 크기와 저장형식을 정의한 것
- 기본형 : 실제 값을 저장
- 논리형(boolean), 문자형(char), 정수형(byte, short, int, long), 실수형(float, double) - 참조형 : 어떤 값이 저장되어 있는 주소를 값으로 저장
- 8개의 기본형을 제외한 나머지 타입
- 참조형 변수를 선언할 때는 변수의 타입으로 클래스의 이름을 사용
- 객체를 생성하는 연산자 new의 결과는 생성된 객체의 주소이다
클래스_이름 변수_이름; // 참조 변수 선언
Date today = new Date(); // Date 객체를 생성해서, 그 주소를 today에 저장
2) 기본형
| 분류 | 타입 |
| 논리형 | boolean |
| true와 false 중 하나를 값으로 갖으며, 조건식과 논리적 계산에 사용된다. | |
| 문자형 | char |
| 문자를 저장하는데 사용되며, 변수에 하나의 문자만 저장할 수 있다. | |
| 정수형 | byte, shrot, int, long |
| 정수를 저장하는데 사용되며, 주로 int가 사용된다. byte는 이진 데이터를 다룰 때 사용되며, short는 C언어와의 호환을 위해서 추가되었다. | |
| 실수형 | float, double |
| 실수를 저장하는데 사용되며, 주로 double이 사용된다. |
- 문자형인 char는 문자를 내부적으로 정수(유니코드)를 저장함
- boolean은 다른 기본형과의 연산이 불가능함
- boolean을 제외한 나머지 7개의 기본형은 서로 연산과 변환이 가능함
| 1 byte | 2 byte | 4 byte | 8 byte | |
| 논리형 | boolean | |||
| 문자형 | char | |||
| 정수형 | byte | short | int | long |
| 실수형 | float | double |
- boolean은 true와 false 두 가지 값만 표현할 수 있으면 되므로 가장 작은 크기인 1byte
- char은 자바에서 유니코드(2 byte 문자체계)를 사용하므로 2byte
- byte는 크기가 1byte라서 byte
- int(4 byte)를 기준으로 짧아서 short(2 byte), 길어서 long(8 byte)
- float는 실수값을 부동 소수점 방식으로 저장하기 때문에 float
- double은 float보다 두 배의 크기를 갖기 떄문에 double

- 정수형의 경우, 범위는 -2^(n-1) ~ 2^(n-1)-1 (n은 bit수, 1byte는 8bit)
- int 타입의 변수는 대략 10자리 수의 값을 저장할 수 있기에,
7~9자리의 수를 계산할 때는 long 타입(약 19자리)로 변수를 선언하는 것이 좋다
- 실수형은 정수형과 저장형식이 달라 같은 크기라도 훨씬 큰 값을 표현할 수 있지만 오차가 발생할 수 있는 단점
(float의 정밀도는 7자리, double의 정밀도는 15자리 : float의 경우, 10진수로 7자리의 수를 오차없이 저장 가능)
3) 상수와 리터럴
- 상수 : 변수와 마찬가지로 값을 저장할 수 있는 공간
- 한 번 값을 저장하면 다른 값으로 변경할 수 없다
- 변수의 타입 앞에 키워드 final을 붙이면 된다
- 반드시 선언과 동시에 초기화해야 한다
- 상수의 이름은 모두 대문자로 하는 것이 암묵적 관례이며, 여러 단어의 경우 '_'로 구분해야 한다
final int MAX_SPEED = 10;
final int MAX_VALUE; // 에러
MAX_VALUE = 100; // 에러
- 리터럴 : 그 자체로 값을 의미하는 것
int year = 2025;
final int MAX_VALUE = 100;
변수 : year
상수 : MAX_VALUE
리터럴 : 2025, 100- 정수형의 경우, long 타입의 리터럴에 접미사 'l' 또는 'L'을 붙이고 접미사가 없으면 int 타입의 리터럴이다
- 실수형의 경우, float 타입의 리터럴에 접미사 'f' 또는 'F'를 붙이고 접미사가 없으면 double 타입의 리터럴이다
- 리터럴에 소수점이나 10의 제곱을 나타내는 기호(E, e). 접미사 f, F, d, D를 포함하고 있으면 실수형 리터럴이다
- 타입이 달라도 저장범위가 넓은 타입에 좁은 타입의 값을 저장하는 것은 허용된다
- 리터럴의 값이 변수의 타입의 범위를 넘거나, 리터럴의 타입이 변수의 타입보다 저장범위가 넓으면 컴파일 에러
double d = 3.14f; // OK. float타입보다 double의 타입 값이 더 범위가 넓다
float f = 3.14; // 에러. float 타입보다 double 타입의 범위가 넓다
int i = 0x123456789; // 에러. int 타입의 범위를 넘는 값을 저장
- 문자 리터럴 : 'A'와 같이 작은 따옴표로 문자 하나를 감싼 것
- 문자열 리터럴 : 두 문자 이상을 큰 따옴표로 감싼 것
- char 타입의 변수는 단 하나의 문자만, String 타입은 여러 문자를 저장 가능
- 문자열 리터럴은 "" 안에 아무런 문자도 넣지 않는 것을 허용(빈 문자열)
- 문자 리터럴은 반드시 하나의 문자가 존재해야 함
// 문자와 문자열 저장
char ch = 'J';
String name = "Java";
String name = new String("Java");
String str = ""; // OK. 빈문자열 허용
char ch = ''; // 에러. 빈문자열 허용 안함
char ch = ' '; // OK. 공백 문자
- 덧셈 연산자는 왼쪽에서 오른쪽으로 연산을 수행하기 때문에 결합 순서에 따라 결과가 달라진다
문자열 + any type = 문자열
any type + 문자열 = 문자열
7 + " " = "7 ";
7 + 7 + "" = "14";
"" + 7 + 7 = "77";
4) 형식화된 출력 - printf()
- 지시자 : 값을 어떻게 출력할 것인지를 지정해주는 역할
- printf() : 지시자를 통해 변수의 값을 여러 가지 형식으로 변환하여 출력
System.out.println("age : %d, year : %d", age, year);
| 지시자 | 설명 |
| %n | 줄바꿈 |
| %b | boolean 형식으로 출력 |
| %d | 10진(decimal) 정수 형식으로 출력 |
| %o | 8진(octal) 정수 형식으로 출력 |
| %x, %X | 16진(hexa-decimal) 정수 형식으로 출력 |
| %f | 부동 소수점 형식으로 출력 |
| %e, %E | 지수 표현 형식으로 출력 |
| %g | 실수형 값을 간략하게 출력 |
| %c | 문자로 출력 |
| %s | 문자열로 출력 |
System.out.printf("finger = [%5d]", finger); // finger = [ 10]
System.out.printf("finger = [%-5d]", finger); // finger = [10 ] 왼쪽 정렬
System.out.printf("finger = [%05d]", finger); // finger = [00010]
System.out.printf("hex=%x", hex); // hex = fffffffff
System.out.printf("hex=%#x", hex); // hex = 0xfffffffff
System.out.printf("hex=%#X", hex); // hex = 0XFFFFFFFFF
System.out.printf("d = %14.10f", d); // 전체 14자리 중 소수점 10자리로 출력
// %f는 기본적으로 소수점 아래 6자리까지만 출력
// 소수점 7자리에서 반올림
System.out.printf("[%.8s]", url); // 왼쪽에서 8글자만 출력
5) 화면에서 입력 받기 - Scanner
nextLiine()이라는 메서드를 호출하면 입력 대기 상태에 있다가 입력을 마치고 엔터키를 누르면 입력한 내용이 문자열로 반환된다.
import java.util.*;
Scanner sc = new Scanner(System.in);
String input = sc.nextLine();
3. 진법
1) 10진법과 2진법
손가락 개수가 10개인 사람에게 10진법이 적합하든, 컴퓨터와 같은 전기회로에는 2진법이 적합하다.
변수에 값을 저장하면 10진수로 저장되는 것 같지만, 컴퓨터는 2진수(0과 1) 밖에 모르기 때문에 해당 10진수를 2진수로 바꾸어서 저장한다. 하지만 2진법은 0과 1로만 데이터를 표현하기 때문에 10진법에 비해서 많은 자리 수를 필요로 한다.
2) 비트(bit)와 바이트(byte)
- 비트(bit) : 한자리 2진수.
컴퓨터가 값을 저장할 수 있는 최소 단위 - 바이트(byte) : 1비트 8개를 묶음.
데이터의 기본 단위 - 워드(word) : CPU가 한 번에 처리할 수 있는 데이터의 크기

1 bit로 표현 가능한 10진수는 0과 1 총 2개이고, 2 bit로 표현 가능한 10진수는 00, 01, 10, 11로 0,1,2,3 총 4개이다.
이것을 일반화하면 다음과 같이 표현할 수 있다.
n비트로 표현할 수 있는 10진수
- 값의 개수 : 2^n
- 값의 범위 : 0 ~ 2^n - 1
3) 8진법과 16진법
2진법으로 값을 표현하면 자리수가 상당히 길어진다는 단점이 존재하는데. 이 단점을 보완하기 위해 2진법 대신 8진법과 16진법을 사용한다. 8진수는 2진수 3자리를, 16진수는 2진수 4자리를 각각 한자리로 표현할 수 있기 때문에 자리수가 짧아져서 알아보기 쉽고 서로 간의 변환방법 또한 매우 간단하다.
8진법은 값을 표현하는데 8개의 기호가 필요하므로 0~7의 숫자를 기호로 사용하고,
16진법은 0~9의 숫자와 추가로 6개의 문자(A~F)를 사용한다.
- 2진수를 8진수로 변환
2진수를 뒤에서부터 3자리씩 끊어서 그에 해당하는 8진수로 바꾸면 된다
ex) 010001(2) -> 21(8) - 2진수를 16진수로 변환
2진수를 뒤에서부터 4자리씩 끊어서 그에 해당하는 16진수로 바꾸면 된다
ex) 10100011(2) -> A3(16)
4) 정수의 진법 변환
- 10진수를 n진수로 변환
10진수를 다른 진수로 변환하려면, 해당 진수로 나누고 나머지 값을 옆에 적는 것을 더 이상 나눌 수 없을 때까지 반복한 다음 마지막 몫과 나머지를 아래부터 위로 순서대로 적으면 된다. 즉, n진수로 변환하려면 n으로 반복해서 나누기만 하면 되는 것이다.
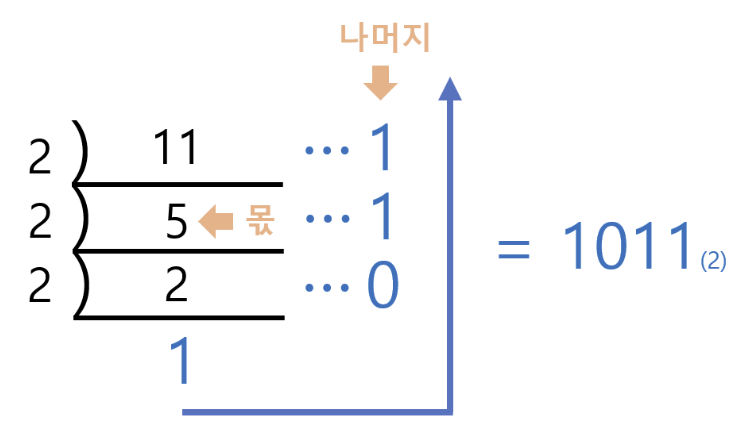
- n진수를 10진수로 변환
각 자리의 수에 해당하는 단위의 값을 곱해서 모두 더하면 된다
10진수를 10진수로
123(10) = 1 * 100 + 2 * 10 + 3 * 1
2진수를 10진수로
101(2) = 1 * 4 + 0 * 2 + 1 * 1
8진수를 10진수로
011(8) = 0 * 64 + 1 * 8 + 1 * 1
5) 실수의 진법 변환
- 10진 소수점수를 2진 소수점수로 변환하는 방법
10진 소수점수를 2진 소수점수로 변환하는 방법은 10진 소수점수에 2를 계속 곱하는 것이다.
(1) 10진 소수에 2를 곱한다
0.625 * 2 = 1.25
(2) 위의 결과에서 소수부만 가져다가 다시 2를 곱한다
0.625 * 2 = 1.25
0.25 * 2 = 0.5
(3) (1)과 (2)의 과정을 소수부가 0이 될 때까지 반복한다
0.625 * 2 = 1.25
0.25 * 2 = 0.5
0.5 * 2 = 1.0
위의 결과에서 정수부만을 위에서 아래로 순서대로 적고 앞에 '0.'을 붙이면 된다
0.625 * 2 = 1.25
0.25 * 2 = 0.5
0.5 * 2 = 1.0
0.625(10) => 0.101(2)
- 2진 소수점수를 10진 소수점수로 변환하는 방법
0.101(2)를 10진 소수점수로 변환
0.101 = 1 * 2^(-1) + 0 * 2^(-2) + 1*2^(-3)
6) 음수의 2진 표현 - 2의 보수법
2의 보수법
어떤 수의 'n의 보수'는 더했을 때 n이 되는 수를 말한다.
'2의 보수 관계'에 있는 두 2진수를 더하면 '(자리 올림이 발생하고)' 0이 된다.
2의 보수법에 의해 음수를 배치하면, 절대값이 같은 양수와 음수를 더했을 때 2진수로도 0을 결과로 얻으므로 부호를 신경쓰지 않고 덧셉을 할 수 있게 된다. 그리고 2진수가 증가할 때 10진 음수가 감소한다는 모순도 사라진다.
| 2진수 | 부호 있는 10진수 |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | -8 |
| 1001 | -7 |
| 1010 | -6 |
| 1011 | -5 |
| 1100 | -4 |
| 1101 | -3 |
| 1110 | -2 |
| 1111 | -1 |
음수를 2진수로 표현하기
10진 음의 정수를 2진수로 변환하려면, 먼저 10진 음의 정수의 절대값을 2진수로 변환한다. 그 다음에 2진수의 '2의 보수'를 구하면 된다
-5(10) --(절대값)--> 5(10) --(2진수)--> 0101(2) --(2의 보수)--> 1011(2)
2의 보수 구하기
서로 '2의 보수'의 관계에 있는 두 수를 더하면 '0(자리올림 발생)'이 된다. 하지만 자리수가 많아지면 이런 식으로 2의 보수를 구하는 것도 쉽지 않아진다.
이 방법보다 더 쉽게 구하는 방법이 존재한다. '1의 보수'를 구한 다음 1을 더하는 것이다.
'1의 보수'는 0을 1로, 1을 0으로 바꾸는 것이다.
0101(2)의 2의 보수 구하기
(1) 1의 보수로 변환하기 -> 1010(2)
(2) 1을 더하기 -> 1010 + 1 = 1011(2)
왜 '1의 보수+1'은 '2의 보수'인가?
어떤 2진수가 있을 때, 이 2진수의 1의 보수를 더하면 모든 자리가 1이 된다.
0101 + 1010(0101의 1의 보수) = 1111
위의 식에서 1을 더하면 올림이 발생하지만 4비트를 넘는 값이라 저장할 공간이 없어져 버려지기에 결국 0이 된다.
따라서 어떤 수에 '1의 보수+1'을 하면 0이 되므로 '1의 보수+1'은 '2의 보수'가 된다
음수의 2진 표현을 구하는 방법
(1) 음수의 절대값을 2진수로 변환한다
-5의 절댓값인 5를 2진수로 변환한다 -> 0101(2)
(2) (1)에서 구한 2진수의 1을 0으로, 0을 1로 바꾼다 (1의 보수 구하기)
0101은 1010이 된다
(3) (2)의 결과에 1을 더한다 (2의 보수 구하기 = 1의 보수 + 1)
1010에다가 1을 더하면 1011이 되고, 이것이 -5의 2진 표현이다
4. 기본형
1) 논리형 - boolean
boolean형 변수에는 true와 false 중 하나를 저장할 수 있으며 기본값은 false이다.
boolean형은 true와 false 두 가지의 값만 표현하면 되므로 1bit만으로도 충분하지만, 자바에서는 데이터를 다루는 최소 단위가 byte이기 떄문에 boolean의 크기가 1byte이다.
자바에서는 대소문자가 구별되기 때문에 TRUE와 true는 다른 것으로 간주된다는 것에 주의하자
2) 문자형 - char
문자형은 문자를 저장하기 위한 변수를 선언할 때 사용되며, char 타입의 변수는 단 하나의 문자만을 저장할 수 있다
char ch = 'A';위 코드에서 변수에 '문자'가 저장되는 것 같지만, 사실은 문자가 아닌 '문자의 유니코드(정수)'가 저장된다. 컴퓨터는 숫자밖에 모르기 때문에 모든 데이터를숫자로변환하여 저장하는 것이다.
특수문자 다루기
| 특수문자 | 문자리터럴 |
| tab | \t |
| backspace(지우기) | \b (ex : "123\b456" -> "12456") |
| form feed | \f |
| new line | \n |
| carriage return | \r |
| 역슬래쉬 | \\ |
| 작은 따옴표 | \' |
| 큰 따옴표 | \" |
| 유니코드(16진수) 문자 | \u유니코드 (ex: char a = '\u0041') |
char 타입의 표현 형식
char 타입의 크기는 2 byte(=16 bit)이므로 총 65536(2^16)개의 정수를 표현할 수 있으며, char 형 변수는 이 범위 내의 코드 중 하나를 저장할 수 있다.
char 타입의 변수에는 문자가 아닌 '문자의 유니코드(정수)'가 저장되고 표현형식 역시 정수형과 동일하다. 다만, 정수형과 달리 음수를 나타낼 필요가 없으므로 표현할 수 있는 값의 범위가 다르다.
16비트로 표현할 수 있는 정수의 개수 : 2^16개 (65536개)
short 타입의 표현 범위 : -2^15 ~ 2^15-1 (-32768 ~ 32767)
char 타입의 표현 범위 : 0 ~ 2^16-1 (0 ~ 65535)
인코딩과 디코딩 (encoding & decoding)
- 인코딩(encoding) : 문자를 코드로 변환하는 것
- 디코딩(decoding) : 코드를 문자로 변환하는 것
문자 'A'의 유니코드가 65이다. 그래서 문자 'A'를 유니코드로 인코딩하면 65가 되는 것이고, 65를 유니코드로 디코딩하면 'A'가 되는 것이다.
아스키(ASCII)
ASCII는 'American Standard Code for Information Interchange'의 약어로 정보 교환을 위한 미국 표준 코드란 뜻이다.
아스키는 128(=2^7)개의 문자집합을 제공하는 7bit부호이다.
아스키는 숫자 '0~9', 영문자 'A~Z'와 'a~z'가 연속적으로 배치되어 있다는 특징이 있다.
3) 정수형 - byte, short, int, long
정수형의 표현형식과 범위
모든 정수형은 부호있는 정수이므로 왼쪽의 첫 번째 비트를 '부호 비트(sign bit)'로 사용하고 나머지는 값을 표현하는데 사용한다.
| 정수형의 표현형식 (n bit) | 종류 | 값의 개수 |
| 0 + (n-1)bit | 0, 양수 | 2^(n-1)개 |
| 1 + (n-1)bit | 음수 | 2^(n-1)개 |
n 비트로 표현할 수 있는 정수의 개수 : 2^n개
n 비트로 표현할 수 있는 부호 있는 정수의 범위 : -2^(n-1) ~ 2^(n-1)-1
정수형의 선택 기준
정수형 변수를 선언할 때는 int 타입으로 하고, int의 범위(약 ±20억)를 넘어서는 수를 다룰 때는 long을 사용하면 된다
2^10 = 1024 = 10^3이므로 2^32 = 4 * 10^9
정수형의 오버플로우
- 오버플로우 : 연산 과정에서 해당 타입이 표현할 수 있는 값의 범위를 넘어서는 것
2진수 '1111'에 1을 더하면 '10000'이 되지만, 4 bit로는 4자리의 2진수만 저장할 수 있기 때문에 '0000'이 된다. 즉, 5자리의 2진수 '10000' 중에서 하위 4 bit만 저장하게 되는 것이다.
정수형 타입이 표현할 수 있는 최대값에 1을 더하면 최소값이 되고, 최소값에서 1을 빼면 최대값이 된다.
최대값 + 1 = 최소값
최소값 - 1 = 최대값
1111 + 1 = (1)0000
0000 - 1 = 1111
부호있는 정수의오버플로우
부호없는 정수와 부호있는 정수는 표현 범위 즉, 최대값과 최소값이 다르기 때문에 오버플로우가 발생하는 시점이 다르다. 부호없는 정수는 2진수로 '0000'이 될 때 오버플로우가 발생하고, 부호있는 정수는 부호비트가 0에서 1이 될때 오버플로우가 발생한다.
4) 실수형 - float, double
실수형의 범위와 정밀도

float 타입의 표현 범위는 '-3.4 * 10^38 ~ 3.4 * 10^38'이지만, '-1.4 * 10^(-45) ~ 1.4 * 10^(-45)' 범위의 값은 표현할 수 없다. 실수형은 소수점수도 표현해야 하므로 '얼마나 큰 값을 표현할 수 있는가' 뿐만 아니라 '얼마나 0에 가깝게 표현할 수 있는가'도 중요하다
정수와 실수는 값을 저장하는 형식이 다르다
int타입은 1bit짜리 부호와 31bit짜리 값으로 구성되어 있지만,
float타입은 1bit짜리 부호(S), 8bit짜리 지수(E), 23bit짜리 기수(M) 총 3부분으로 구성되어 있다.
즉, '2의 제곱을 곱한 형태(±M * 2^E)'로 저장하기 때문에 이렇게 큰 범위의 값을 저장하는 것이 가능하다.
실수형 값을 저장할 때, float 타입이 아닌 double 타입의 변수를 사용하는 경우는 대부분 저장하려는 값의 범위 때문이 아니라 보다 높은 정밀도가 필요해서이다. 연산 속도의 향상이나 메모리를 절약하려면 float을 선택하고, 더 큰 값의 범위라던가 더 높은 정밀도를 필요로 한다면 double을 선택해야 한다.
실수형의 저장 방식
실수형은 값을 부동소수점수(floating-point)의 형태로 저장한다. 부동소수점수는 실수를 '± * 2^E'와 같은 형태로 표현하는 것을 말하며, 부동소수점수는 부호(Sign), 지수(Exponent), 가수(Mantissa) 모두 세 부분으로 이루어져 있다.


1) 부호 (Sign)
S는 부호 비트를 의미하며 1 bit 이다. 이 값이 0이면 양수를, 1이면 음수를 뜻한다.
정수형과 달리 2의 보수법을 사용하지 않기 때문에, 양의 실수를 음의 실수로 바꾸려면 그저 부호 비트만 0에서 1로 바꾸면 된다.
2) 지수 (Exponent)
E는 지수를 저장하는 부분으로, float의 경우 8bit의 저장 공간을 갖는다.
지수는 부호 있는 정수이고 8 bit로는 2^8개의 값을 저장할 수 있으므로 '-127 ~ 128'의 값이 저장된다.
3) 가수 (Mantissa)
M은 실제 값인 가수를 저장하는 부분으로, float의 경우 2진수 23자리를 저장할 수 있다.
2진수 23자리는 약 7자리의 10진수를 저장할 수 있는데 이것이 바로 float의 저밀도가 된다.
5. 형변환
1) 형변환 (캐스팅, casting)이란?
변수 또는 상수 타입을 다른 타입으로 변환하는 것을 의미한다
2) 형변환 방법
형변환하고자 하는 변수나 리터럴의 앞에 변환하고자 하는 타입을 괄호와 함께 붙여주기만 하면 된다
(타입)피연산자
double d = 85.4;
int score = (int)d;
- 형변환 연산자는 그저 피연산자의 값을 읽어서 지정된 타입으로 형변환하고 그 결과를 반환할 뿐이다. 그래서 피연산자인 변수 d의 값은 형변환 후에도 아무 변화가 없다
- 기본형에서 boolean을 제외한 나머지 타입들은 서로 형변환이 가능하다.
- 기본형과 참조형 간의 형변환은 불가능하다.
- float 타입의 값을 int 타입으로 변환할 때 소수점 이하의 값은 반올림이 아닌 버림으로 처리된다
| 변환 | 수식 | 결과 |
| int -> char | (char) 65 | A |
| char -> int | (int) 'A' | 65 |
| float -> int | (int) 1.6f | 1 |
| int -> float | (float) 10 | 10.0f |
3) 정수형 간의 형변환
- 큰 타입에서 작은 타입으로 변환
예를 들어 int 타입의 값을 byte 타입의 값으로 변환하는 경우 크기의 차이만큼 값이 잘려나간다. (값 손실 발생) - 작은 타입에서 큰 타입으로 변환
예를 들어 byte 타입의 값을 int 타입의 값으로 변환하는 경우 저장공간의 부족으로 잘려나가는 일이 없으므로 값 손실이 발생하지 않는다. 그리고 나머지 빈공간은 0 또는 1로 채워진다.
원래 값을 채우고 남은 빈공간은 0으로 채우는게 보통이지만, 변환하려는 값이 음수인 경우에는 빈 공간을 1로 채운다
4) 실수형 간의 형변환
- 작은 타입에서 큰 타입으로 변환
float 타입의 값을 double 타입으로 변환하는 경우, 지수(E)는 float의 기저인 127을 뺀 후 double의 기저인 1023을 더해서 변환하고, 가수(M)은 float의 가수인 23자리를 채우고 남은 자리를 0으로 채운다. - 큰 타입에서 작은 타입으로 변환
지수(E)는 double의 기저인 1023을 뺀 후 float의 기저인 127을 더하고, 가수(M)은 double의 가수 52자리 중 23자리만 저장되고 나머지는 버려진다. 한 가지 주의할 점은 형변환할 때 가수의 24번째 자리에서 반올림이 발생할 수 있다는 것이다. 24번째 자리의 값이 1이면, 반올림이 발생하여 23번째 자리의 값이 1 증가한다
5) 정수형과 실수형 간의 형변환
- 정수형을 실수형으로 변환
정수를 2진수로 변환한 다음에 정규화해서 실수의 저장형식에 맞게 저장할 뿐이다. 한 가지 주의할 점은 실수형의 정밀도의 제한으로 인한 오차가 발생할 수도 있다는 것이다 - 실수형을 정수형으로 변환
실수형을 정수형으로 변환하면, 실수형의 소수점 이하 값은 버려진다. 따라서 반올림은 발생하지 않는다.
만일 실수의 소수점을 버리고 남은 정수가 정수형의 저장범위를 넘는 경우에는 정수의 오버플로우가 발생한 결과를 얻는다
6) 자동 형변환
서로 다른 타입 간의 대입이나 연산을 할 때, 형변환으로 타입을 일치시키는 것이 원칙이다. 하지만, 경우에 따라 편의상의 이유로 형변환을 생략할 수 있다. 그렇다고 해서 형변환이 이루어지지 않는 것은 아니고, 컴파일러가 생략된 형변환을 자동적으로 추가한다.
float f = 1234; // 형변환의 생략
변수가 저장할 수 있는 값의 범위보다 더 큰 값을 저장하려는 경우에 형변환을 생략하면 에러가 발생한다. 그러나 명시적으로 형변환을 해줬을 경우, 형변환이 프로그래머의 실수가 아닌 의도적인 것으로 간주하고 컴파일러는 에러를 발생시키지 않는다.
byte b = 1000; // 에러
char ch = (char)1000; // 명시적 형변환
서로 다른 두 타입 간의 덧셈에서는 두 타입 중 표현범위가 더 넓은 타입으로 형변환하여 타입을 일치시킨 다음에 연산을 수행한다.
자동 형변환의 규칙
자동 형변환은 기존의 값을 최대한 보존할 수 있는 타입으로 자동 형변환한다.
표현 범위가 좁은 타입에서 넓은 타입으로 형변환하는 경우에는 값 손실이 없으므로 두 타입 중에서 표현범위가 더 넓은 쪽으로 형변환된다
1. boolean을 제외한 나머지 7개의 기본형은 서로 형변환이 가능하다
2. 기본형과 참조형은 서로 형변환할 수 없다
3. 서로 다른 타입의 변수 간의 연산은 형변환을 하는 것이 원칙이지만,
값의 범위가 작은 타입에서 큰 타입으로의 형변환은 생략할 수 있다.